Aggregation
Results are aggregated annually and monthly on the Yield Results tab.
 Yield results tab in Calculation chapter (click to enlarge)
Yield results tab in Calculation chapter (click to enlarge)
The aggregation method depends on the field as summarized in the following table.
| Field | Aggregation | Units |
|---|---|---|
| Record Count | sum | |
| Complete | time-weighted average | % |
| Energy Yield | sum | kWh/kWp |
| Grid Energy | sum | MWh/year |
| Performance Ratio | time-weighted average | % |
| Bifacial Performance Ratio | time-weighted average | % |
| Production DC | sum | kWh |
| Production AC | sum | kWh |
| GHI | sum | kWh/m² |
| GI | sum | kWh/m² |
| Global Effective Insolation | sum | kWh/m² |
| Temperature | time-weighted average | °C |
| Gain on the Tilted Plane | time-weighted average | % |
(See the Yield Results page for a description of each field.)
Time Averaging
For results that are intrinsic, such as completeness, performance ratio, temperature, and gain, the aggregated result is a time-weighted average over the period of interest. For example, for field \(X\) the time-weighted average over a specific month with \(N_\text{intervals}\) each of size \(\Delta t_n\) where \(n\) is the index of each interval starting at 1, the average, \(X_\text{avg}\), over the month would be given by the following equation:
$$X_\text{avg} = \frac{\sum_{n=1}^{N_\text{intervals}}{X \left( t_n \right) \Delta t_n }} {\sum_{n=1}^{N_\text{intervals}}{\Delta t_n }}$$
In the case of monthly aggregation, all of the intervals are the same size, so \(\Delta t_n\) cancels out and the equation simplifies.
$$X_\text{avg,month} = \frac{\sum_{n=1}^{N_\text{intervals,month}}{X \left( t_n \right) }} {N_\text{intervals,month}}$$
Aggregate Sum
Extrinsic results like yield, net energy, production, and irradiance accumulate throughout the period, and so the aggregate is simply the sum of that field over all of the intervals in the period.
$$Y_\text{sum} = \sum_{n=1}^{N_\text{intervals}}{Y \left( t_n \right) }$$
Power to Energy
If the result is a quantity of power, \(y\) in watts (W), then the value at the interval center is assumed constant over the interval and transformed to the energy \(Y\) in watt-hours (Wh) for that entire interval by multiplying the power by the size of the interval, \(\Delta t\) in hours (h).
$$Y_\text{sum} \left[ \text{Wh} \right] = \sum_{n=1}^{N_\text{intervals}} {y \left( t_n \right) \left[ \text{W} \right] \Delta t_n \left[ \text{h} \right] }$$
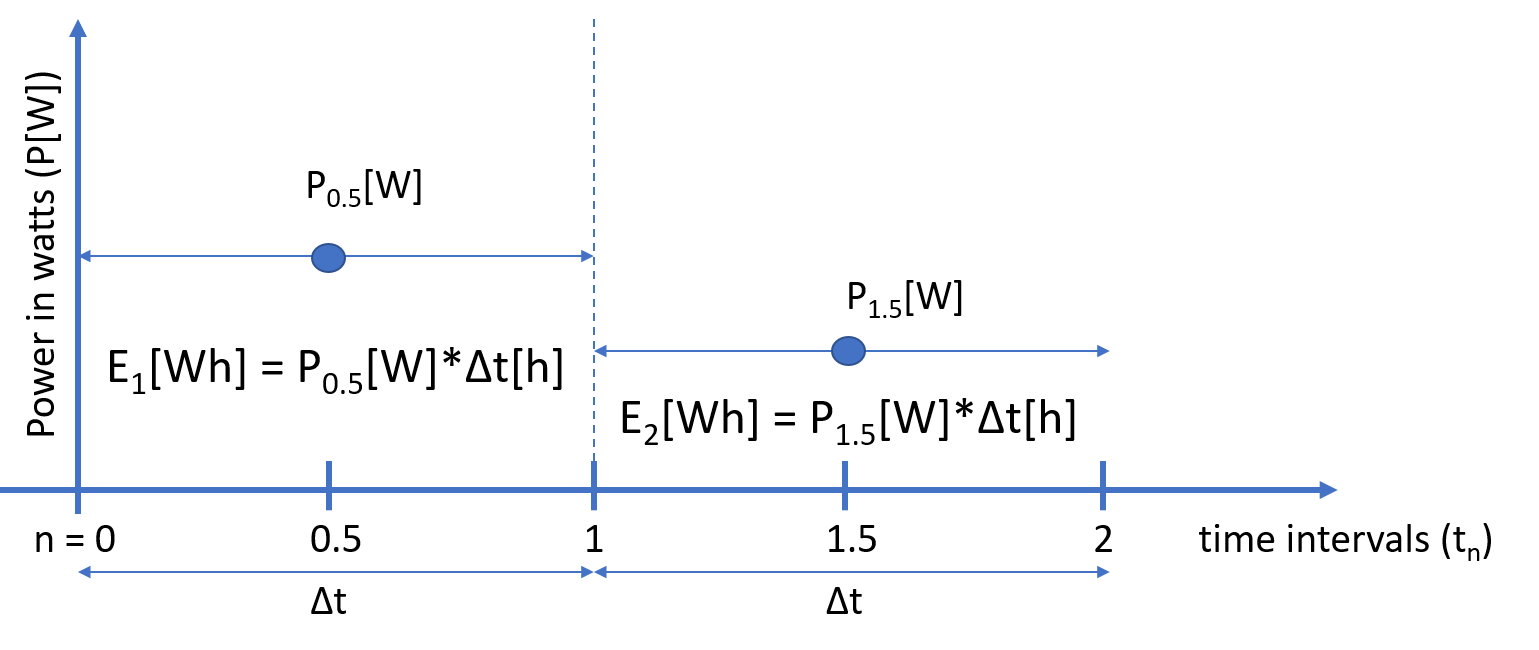 Relation between power, energy, and time intervals
Relation between power, energy, and time intervals
Whether or not the energy corresponds to the beginning, end, or middle of the interval depends on the type of input resource, but power will always correspond to the center of the interval.
TMY Results
If the input resource is in the format of a typical meteorological year (TMY) then the Annual Results will only have a single row, with the selected Calculation year from the Calculation tab. The Monthly Results contain the aggregated totals for each month of the year.
Non-TMY Results
If the input resource is less than a single year or contains a span greater than a year, then all of the years in the span are included in the Yield Results, and the Complete (%) column indicates what fraction of the year and month are missing.