Inverter Efficiency Model
Inverter efficiency is usually the most significant cause of inverter-related energy losses. Inverter efficiency data are supplied in two forms:
Maximum and Weighted efficiencies (including whether these are European or CEC values). In this case, the voltage at which these efficiencies apply will probably not be specified, but can be assumed to be the voltage at which the inverter achieves its highest efficiency.
California Energy Commission (CEC) measured efficiency curves. These are typically measured at three input voltages and at six power levels between 10% and 100% of the rated maximum power.
A function giving inverter efficiency as a function of DC Power and DC Voltage is fitted through these data as described in the sections below on Maximum and Weighted Efficiencies and CEC Measured Efficiency Curves. We denote the inverter efficiency (in %, from 0%-100%) as \(\eta_\text{inv}\). Where only maximum and weighted efficiencies are available, efficiency is a function of DC power \(\eta_\text{inv}\left(P_\text{DC}\right)\); where measured efficiency curves at a range of voltages are available, efficiency is a function of DC power and voltage \(\eta_\text{inv}\left(P_\text{DC}, V_\text{DC}\right)\).
The inverter maximum power curve is first established from the inverter model at a set of \(V_\text{dc}\) values by evaluating inverter efficiency at each voltage and 100% AC output power level, then calculating the corresponding DC power and hence \(I_\text{dc}\) value.
For a derivation ad discussion of the formulae included in this section, see [3].
An example of the variation of inverter efficiency is shown here (in this case at a three different voltages, from a CEC inverter test result):
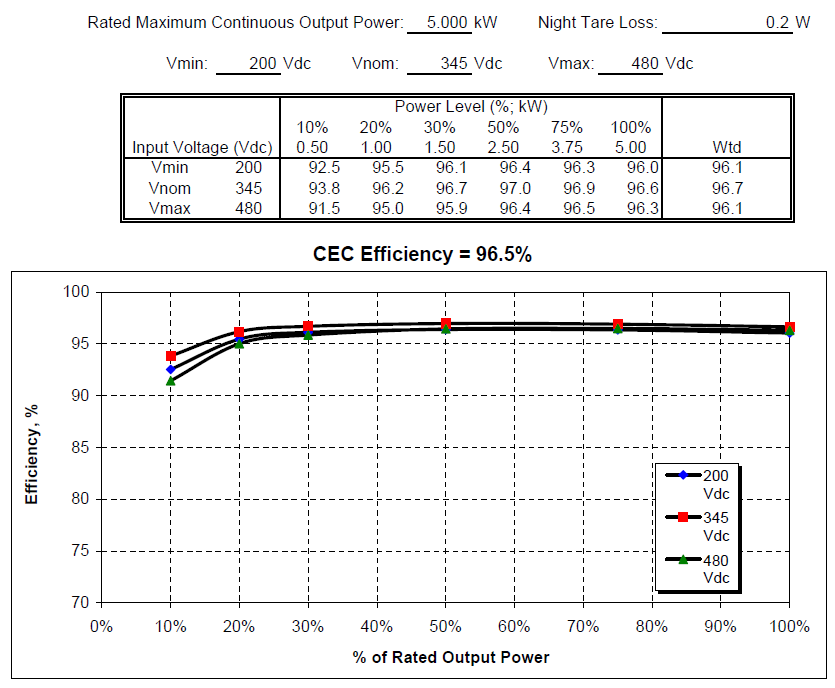
At a particular voltage, a "Weighted" ("Wtd" in the table above) efficiency is calculated from the measured efficiencies at different power levels. CEC and "European" weightings are intended to reflect the likely operating regime of inverters in each region, and are as follows:
$$\eta_\text{CEC} = 0.04 \eta_{10\%} + 0.05 \eta_{20\%} + 0.12 \eta_{30\%} + 0.21 \eta_{50\%} + 0.53 \eta_{75\%} + 0.05 \eta_{100\%}$$
$$\eta_\text{EU} = 0.03 \eta_{5\%} + 0.06 \eta_{10\%} + 0.13 \eta_{20\%} + 0.10 \eta_{30\%} + 0.48 \eta_{50\%} + 0.20 \eta_{100\%}$$
Maximum and Weighted Efficiencies
Where only the maximum and weighted efficiencies of the inverter have been specified by the user, the power consumed by the Inverter at DC Power level \(P_\text{DC}\) is:
$$\Delta P_\text{inv} \left( P_\text{DC} \right) = \left( L_\text{tr} P_\text{inv,rating} + L_\text{dr} P_\text{DC} + \frac{ P_\text{DC}^2}{L_\text{rr} P_\text{inv,rating}} \right)$$
Where \(P_\text{inv,rating}\) is the rated (maximum) AC output power of the inverter.
Then the inverter efficiency \(\eta\) at a given DC Power level \(P_\text{DC}\) is given by:
$$\eta_\text{inv} \left( P_\text{DC} \right) = 1 - \frac{\Delta P_\text{inv} \left( P_\text{DC} \right)} {P_\text{DC}}$$
European Weighted Efficiency
- \(L_\text{tr} = \frac{3600}{5071}\left( \eta_\text{max} - \eta_{wtd,EU} \right)\) is the tare loss
- \(L_\text{dr} = 1 - \frac{10}{3} L_\text{tr} - \eta_\text{max}\) is the diode loss
- \(L_\text{rr} = \frac{36}{100 L_\text{tr}}\) is the resistive loss
CEC Weighted Efficiency
- \(L_\text{tr} = \frac{1200}{677}\left( \eta_\text{max} - \eta_{wtd,CEC} \right)\) is the tare loss
- \(L_\text{dr} = 1 - \eta_\text{max} - \frac{3200}{677}\left( \eta_\text{max} - \eta_{wtd,CEC} \right)\) is the diode loss
- \(L_\text{rr} = \frac{677}{2000\left( \eta_\text{max} - \eta_{wtd,CEC} \right)}\) is the resistive loss
CEC Measured Efficiency Curves
Where a full set of CEC measured efficiency curves are available for an inverter, the efficiency at a given DC Power level and voltage can be estimated.The derivation of parameters to use in calculating inverter efficiency are given in the Sandia Grid inverter model [25].
$$P_\text{ac} = P_\text{dc} \Delta P_\text{inv} \left( P_\text{DC}, V_\text{DC} \right)$$
Maximum DC Power as a function of DC Voltage
In order to apply the inverter AC (output) power limit at the inverter inputs when assessing the effect of this limit on Array performance as described in Maximum AC Power, it is necessary to derive a curve of DC current as a function of DC voltage for which the inverter output equals the AC power limit, \(P_\text{inv,DC,max}\left(V\right)\), taking the inverter efficiency into account at each point. Where inverter efficiency is known as a function of power only (see Maximum and Weighted Efficiencies).