Coordinate systems
Universal Transverse Mercator (UTM) coordinate system
The starting point for defining the layout in 3D is typically with the UTM coordinates, along with an elevation. This forms a right-handed Cartesian X,Y,Z system by mapping the northing to Y, the easting to X, and the elevation to Z. The origin of this system depends on the UTM zone and is different for Northern and Southern hemisphere. For Northern hemisphere the origin is on the equator, 500000m West of the central zone's central meridian.
Longitude, Latitude.
The solar position algorithm is based on the location of the site, specified as a longitude and latitude rather than using a UTM projection. The solar position calculation returns the solar azimuth and zenith. The azimuth is defined from True North so can be used to calculate shading and incidence angles on systems defined in the site reference frame as that frame is also aligned with True North.
Site reference frame and True North.
The UTM coordinate system has two draw-backs that need addressing before proceeding with the energy calculation. The origin is a long way from the system, which can cause issues with numerical precision. It is not aligned with True North. There is a small difference between True North and Grid North, known as the (convergence angle)[https://en.wikipedia.org/wiki/Transverse_Mercator_projection#Convergence]
Therefore we use a site reference frame as the starting point for the calculations. The origin of X and Y coordinates is shifted to a central point for the site. SF does not yet include a correction for the convergence angle, but it is on the roadmap. Therefore until that improvement in SF is made, when doing 3D calculations, the user should be aware that they will get better accuracy by aligning the racks and trackers with True north, and accepting that they are not exactly where they should be on the map.
In the site reference frame we commonly use polar coordinates, for example for defining the solar position, the system azimuth or the terrain slope. The azimuth is always measured clockwise from North, and the zenith is the angle from the vertical. For example when the sun sets in the West it will have an azimuth of 270deg and a zenith of 90deg. The zenith can also be specified as -90deg, all the calculations in SF should work equally well using either convention.
Note, this, clockwise from North convention is not the more typical, pure mathematical definition of azimuth which has 0 being aligned with the x-axis and positive azimuth being a positive rotation around the z axis.
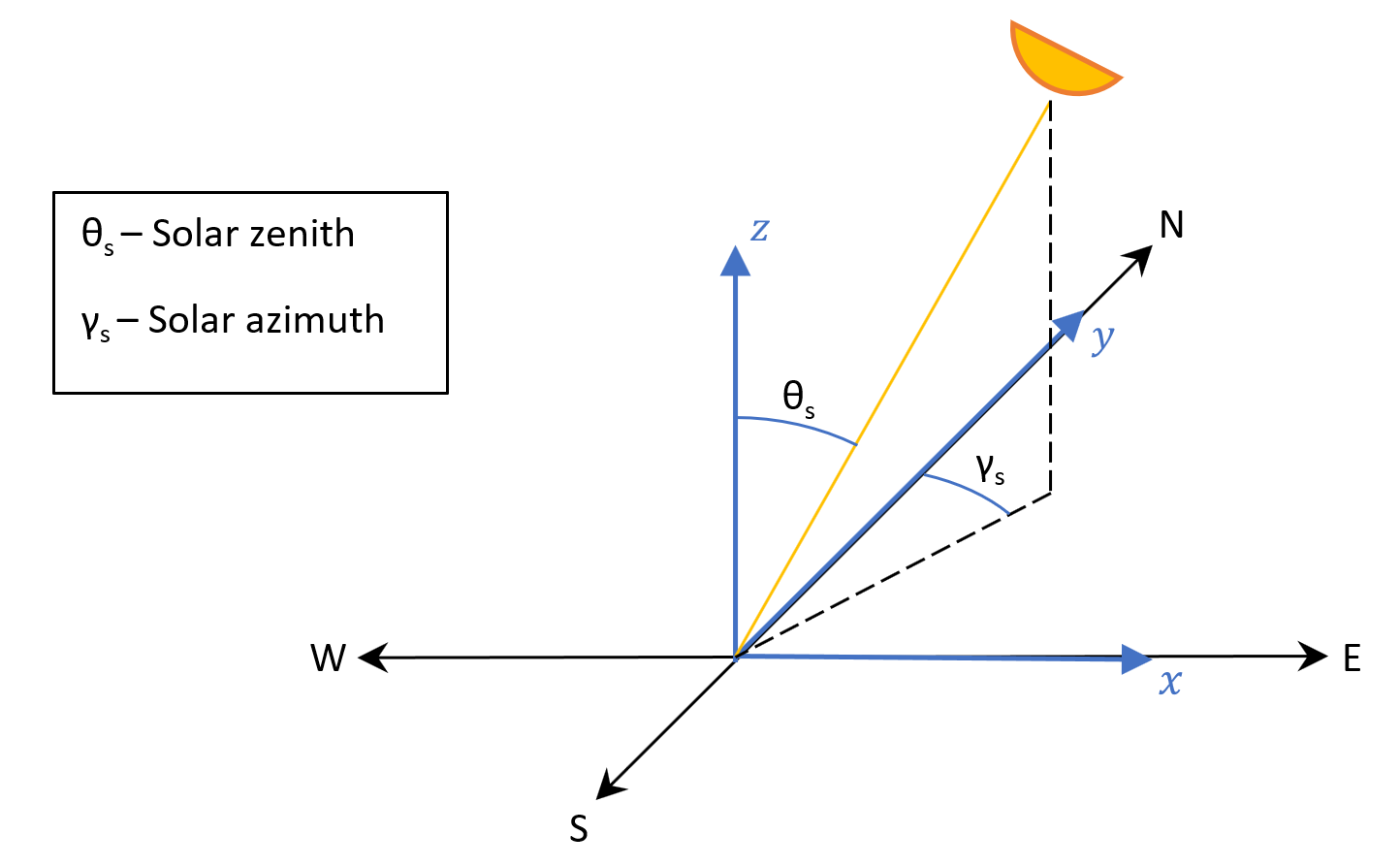 Site reference frame
Site reference frame
System azimuth reference frame
Used for: defining the pitch, defining the along-row slope, defining the along-row reference frame
This is simply the site reference frame rotated about the z axis to align with the system azimuth. The x-y plane is still perfectly horizontal. The y-axis points approximately along the rows and the x-axis points towards the front of the array. Therefore for a fixed tilt system, the system azimuth frame is formed by rotating the site frame about the z axis by the system azimuth minus 90 degrees. For a tracker system the frame switches around 180 degrees between morning and afternoon. When the trackers are rotated to the right the frame is formed by rotating by the tracker system azimuth, when the trackers are rotated to the left we rotate by an additional 180 degrees.
The x and y axes are strictly horizontal so for a site with a terrain slope the y-axis is not exactly aligned with the tracker axis or rack tops, but appears aligned when view from above. The along-row slope is defined as the angle between the y-axis and the tracker axis or rack tops. The along-row slope is positive for slopes that go down in the positive y direction.
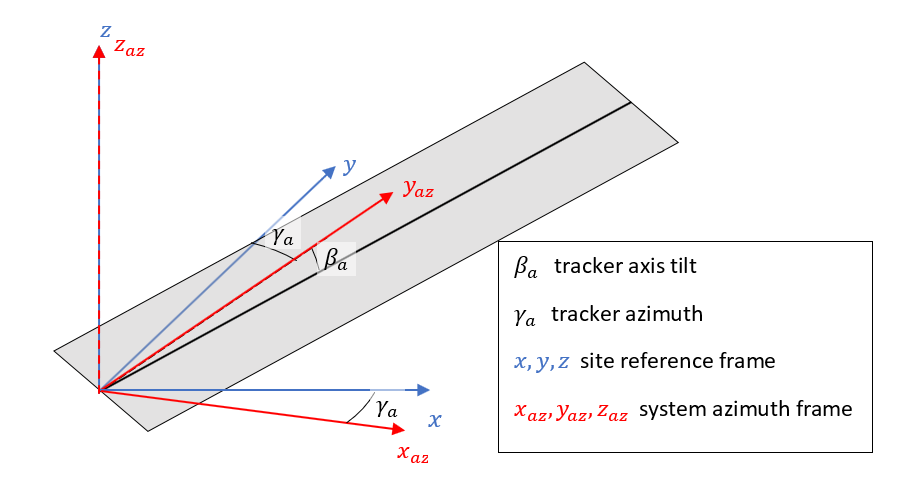 System azimuth reference frame
System azimuth reference frame
Along-row reference frame or Tracker Axis reference frame
Used for: calculating the tracker angle, defining the tilt of a fixed-tilt system, defining the system-plane reference frame, defining the forward slope
This is system azimuth reference frame rotated in the negative x direction by the along row slope. This brings the y-axis into alignment with the tracker axes or rack tops.
![]() Along-row reference frame for a tracker system (tracker axis reference frame)
Along-row reference frame for a tracker system (tracker axis reference frame)
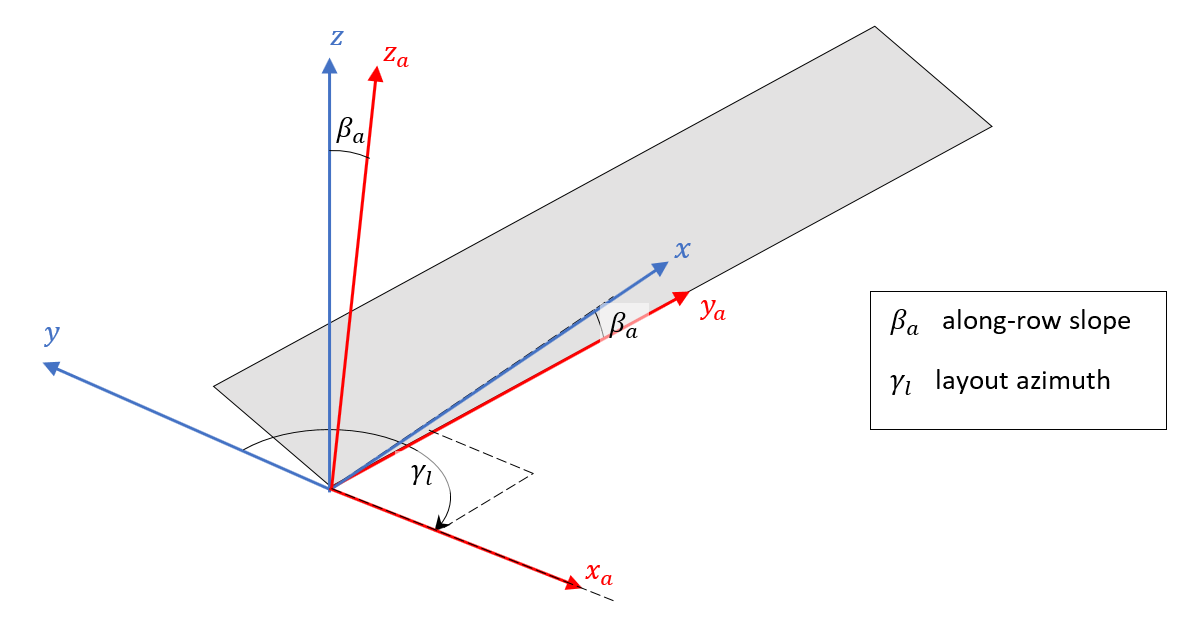 Along-row reference frame for a fixed tilt system
Along-row reference frame for a fixed tilt system
The x-axis remains horizontal in this frame. And it is from this horizontal reference that we define the tracker angle of rotation, the tilt of a fixed-tilt system and the terrain forward slope. Because the y-axis now tilts with any along-row slope, the plane of the modules meets the x-z plane of this frame perpendicularly.
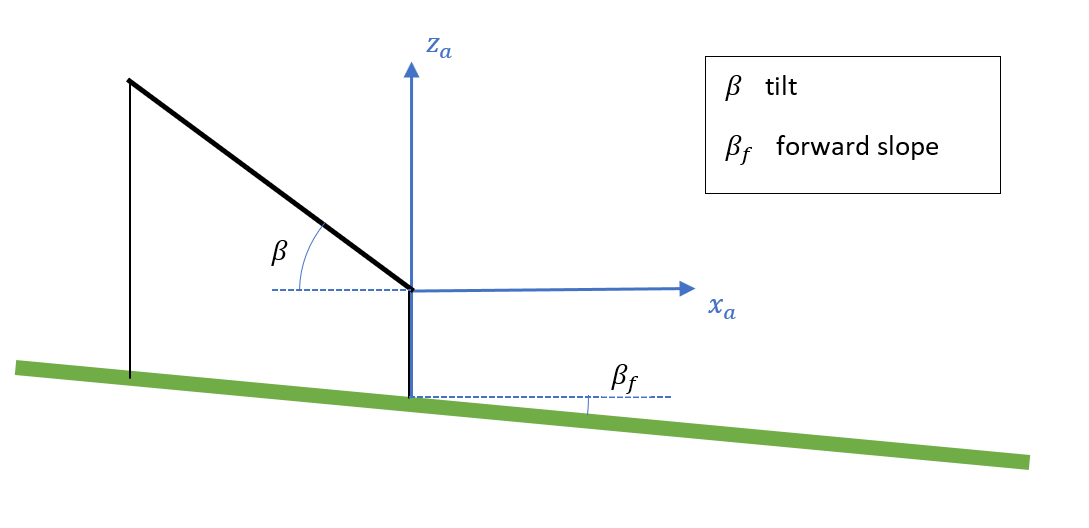 Tilt and forward slope defined in along-row frame
Tilt and forward slope defined in along-row frame
Note that this diagram is not a view horizontally, but a view tilted by the along-row slope. The plane of the modules is tilted from the horizon by both the tilt angle seen here and any along-row slope. This leads to an effective tilt, for the purpose of the plane-of-array irradiance calculation, that can be greater than the system tilt.
System plane reference frame
Used for: performing the 2D shading model
The system plane reference frame is formed by rotating the along-row frame around the y-axis by the forward slope. The takes the x-axis off the horizontal and aligns it with the "system plane", i.e. the plane that contains all the tracker axes or all the bottom edges of the racks. In a model that includes undulating terrain, the trackers or racks may not lie in a plane, in that case each tracker or rack has it's own system plane that follows the terrain at that location. The system plane is an idealisation that is used in the 2D shading model and is used in the tracker position algorithm.
As the system plane reference frame is rotated forwards or backwards by the forward slope the apparent module tilt or tracker rotation is reduced by the forward slope angle. The 2D shading calculation in SolarFarmer includes this effect. It always uses the tilt in the system plane frame, the "sloped tilt". The 2D shading calculation also includes a correction to account for the fact that the apparent GCR is different in the system plane frame. The pitch specified in the inputs is taken as only the horizontal component of the distance between rows, so the total distance is greater by \(\frac{1}{\cos(\beta_{f})}\) and the GCR is smaller by a factor of \(\cos(\beta_{f})\).
The system plane reference frame